排序(Sort)是将无序的记录序列(或称文件)调整成有序的序列。
10.1排序分类
按照排序的稳定性可以将排序分为稳定排序和非稳定排序。按照排序的存储可分为内排序和外排序。
1、稳定排序和非稳定排序
设待排文件f = (R1 R2 ……….. Rn)相应的 key 集合为k = {k1 k2 ……..kn },且在排序前的序列中Ri 领先于 Rj (即i < j )。若在排序后的序列中, Ri 仍领先Rj ,则称所用的排序方法是稳定的;反之,若可能使排序后的序列中 Rij领先于 Ri ,则称所用的排序方法是不稳定的。
2、内排序和外排序
内部排序:若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。【衡量内排序的效率是数据的比较次数】
外部排序:若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。【衡量外排序的效率是内存与外存的交换次数】
总之,在排序的过程中需进行下列两种基本操作:
1) 比较两个关键字的大小 ;
2)将记录从一个位置移动到另一个位置。
外排序是在内排序的基础上进行排序,下面我们给出内排序的算法分类图。
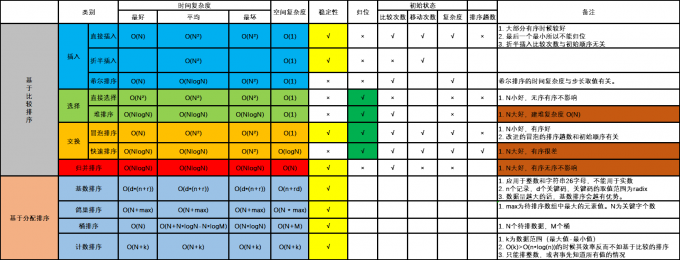
10.2插入排序
10.2.1直接插入排序
直接排序是一种最简单的排序方法,它的基本操作是将一个记录插入到已排好序的有序表中,从而得到一个新的、记录数增1的有序表;
设待排文件f = (R1 R2 ……….. Rn)相应的 key 集合为k = {k1 k2 ……..kn },其排序方法是:
现将文件中的(R1)看成只含一个记录的有序子文件,然后从R2起,逐个将 R2 至 Rn按key插入到当前有序子文件中,最后得到一个有序的文件。插入的过程是一个key的比较过程,即每插入一个记录时,将其key 与当前有序字表中的key进行比较,找到待插入记录的位置后,将其插入即可。
#define maxsize 1024 //文件最大长度
typedef int key_t; //设key为整数
typedef struct //记录类型
{
key_t key; //记录关键字
..... //记录其他域
}Retype;
typedef struct //文件或表的类型
{
Retype R[maxsize + 1]; //文件存储空间
int len; //当前记录数
}sqfile; 若说明sqfile F ; 则(F.R[1],F.R[2],。。。F.R[F.len] )为待排文件,它是一种顺序结构;文件长度 n = F.len ;F.R[0] 为工作单元,起到“监视哨”的作用;记录的关键字ki 写作 F.R[i].key 。
算法描述:
void Insort(sqfile F)
{
int i,j;
for(i = 2;i <= F;i++) //插入n - 1个记录
{
F.R[0] = F.R[i]; //带插入记录先存于监视哨
j = i - 1;
while(F.R[0].key < F.R[j].key) //key 比较
{
F.R[j + 1] = F[j]; //记录顺序后移
j--;
}
F.R[j + 1] = F.R[0]; //原R[i]插入j + 1位置
}
} 排序的时间复杂度取耗时最高的量级,故直接插入排序的T(n) = O(n*n)。
10.2.2折半插入排序
排序算法的T(n) = O(n*n) ,是内排序时耗最高的时间复杂度。随着文件记录数n的增大,效率降低较快,下面的一些插入排序的方法,都是围绕着改善算法的时间的复杂度而展开的。另外,直接插入排序是稳定排序。
为了减少插入排序过程中key的比较次数,可采用折半插入排序。
排序方法:
同直接插入排序,先将(R[1])看成一个子文件,然后依次插入R[2] …..R[n] 。但在插入R[i] 时,子表(R[1] 。。。R[i-1])已是有序的,查找R[i] 在子表中位置可按折半查找方法进行,从而降低key 的比较次数。
算法描述:
void Binsort(sqfile F) //对文件F折半插入排序的算法
{
int i,j,high,low,mid;
for(i = 2;i <= F.len,i++) //插入n-1个记录
{
F.R[0] = F.R[i];//待插入记录存入监视哨
low = 1;
high = i - 1;
while(low < high) //查找 R[i]的位置,即low = high 时;
{
mid = (low + high)/2;
if(F.R[0].key >= F.R[mid].key)
low = mid + 1; //调整下界
else
high =mid - 1;//调整上界
}
for(j = i - 1;j >= low;j--)
F.R[j + 1] = F.R[j]; //记录瞬移
F.R[low] = F.R[0]; //原R[i]插入low位置
}
} 10.3交换排序
10.3.1冒泡排序
设待排文件 f = (R1 R2 … Rn),相应key集合k = {k1 ,k2, ……kn}。
排序方法:
从k1起,两两key比较,逆序时交换,即:
k1~k2,若 k1 > k2 ,则R1 与 R2 交换;
…..
k n-1 ~ kn,若kn-1 > kn ,则Rn-1 与 Rn 交换。
经过一趟比较之后,最大key的记录沉底,类似水泡。接着对前n-1个记录重复上述过程,直到排序完毕。
起泡排序的市价你复杂度 T(n) = O(n*n) 。
算法描述:
void Bubsort(sqfile F)
{
int i,flag; //flag 作为记录交换的标志
Retype temp;
for(i = F.len;i > 2;i--) //最多n - 1次排序
{
flag = 0;
for(j = 1; j <= i - 1;j++) //一趟起泡排序
{
if(F.R[j].key > F.R[j + 1].key) //两两比较
{
temp = F.R[j]; //交换
F.R[j] = F.R[j + 1];
F.R[j + 1] = temp;
flag = 1;
}
flag = 1;
}
if(flag == 0) //无记录交换时排序完毕
break;
}
} 10.3.2快速排序
快速排序的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j–),找到第一个小于key的值A[j],将A[j]和A[i]互换;
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]互换;
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
算法描述:
1)一趟快排算法
int Partition(sqfile *L,int low ,int high)
{
key_t pivotkey; //基准key
L->r[0] = L->r[low]; //存入基准记录
pivotkey = L->r[low].key; //存入基准key
while(low < high)
{
while(low < high && L->r[high].key >= pivotkey) //逆序比较
high--;
if(low < high)
L->r[low] = L->r[high]; //比 pivotkey小的key左移
while(low < high && L->r[low].key <= pivotkey) //正序比较
low++;
if(low < high)
L->r[high] = L->r[low]; //比 pivotkey 大的右移
}
L->r[low] = L->r[0]; //基准记录存入第i位置
return low; //返回基准位置
} 2)对文件L快速排序的算法(递归)
void QSort(sqfile *L,int low ,int high)
{
int pivotloc;
int i;
if(low < high)
{
pivotloc = Partition(L,low,high); //将L分成两部分
QSort(L,low,pivotloc - 1); //对左部再排序
QSort(L,pivotloc + 1,high); //对右部再排序
}
} 下面是个测试程序:
#include <stdio.h>
#define maxsize 1024
typedef int key_t;
typedef struct
{
key_t key;
}Retype;
typedef struct
{
Retype r[maxsize + 1];
int len;
}sqlist;
int Partition(sqlist *L,int low ,int high)
{
key_t pivotkey;
L->r[0] = L->r[low];
pivotkey = L->r[low].key;
while(low < high)
{
while(low < high && L->r[high].key >= pivotkey)
high--;
if(low < high)
L->r[low] = L->r[high];
while(low < high && L->r[low].key <= pivotkey)
low++;
if(low < high)
L->r[high] = L->r[low];
}
L->r[low] = L->r[0];
return low;
}
void QSort(sqlist *L,int low ,int high)
{
int pivotloc;
int i;
if(low < high)
{
pivotloc = Partition(L,low,high);
QSort(L,low,pivotloc - 1);
QSort(L,pivotloc + 1,high);
}
}
int main()
{
int i;
sqlist L;
L.len = 8;
key_t a[8] = {50,36,66,76,36,12,25,95};
for(i = 1; i < 9; i++)
{
L.r[i].key = a[i - 1];
}
printf("Begin sorting!\n");
QSort(&L,1,8);
for(i = 1; i < 9; i++)
{
printf("%d ",L.r[i].key);
}
printf("\n");
return 0;
} 资源获取方法
1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料提取码

